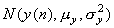
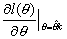 と
と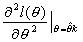 を
を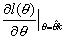 と
と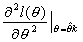 は
は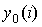
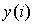
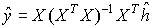
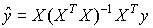
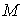 次元実空間
次元実空間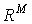
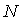 次元実空間
次元実空間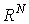
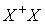
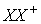
†2 orthogonalは直交の意味で,通常「直交行列」と訳されるが,性質は正 規直交(orthonormal)であるので,本書では「正規直交行列」としている。
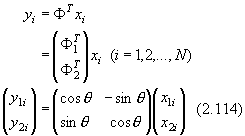
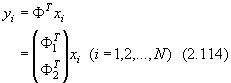
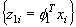
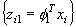
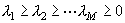
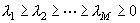
 とから
とから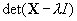
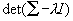
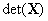
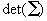
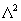 や
や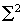 や
や行列Yの列は,
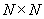 行列
行列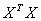 の固有ベクトルとなる。
の固有ベクトルとなる。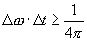 または
または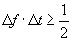
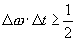 または
または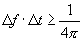
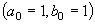
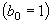
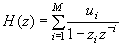
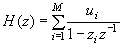
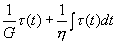
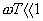 と
と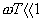 の
の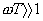 と
と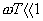 の
の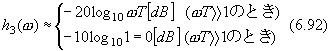
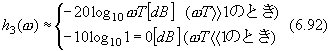
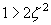 と
と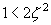 の
の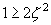 と
と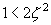 の
の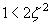 のとき
のとき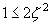 のとき
のとき| 頁 | 該当箇所 | 誤 | 正 |
|---|---|---|---|
| 1 | 6行目 | (least squares method) | (least-squares methodまたはmethod of least squares) |
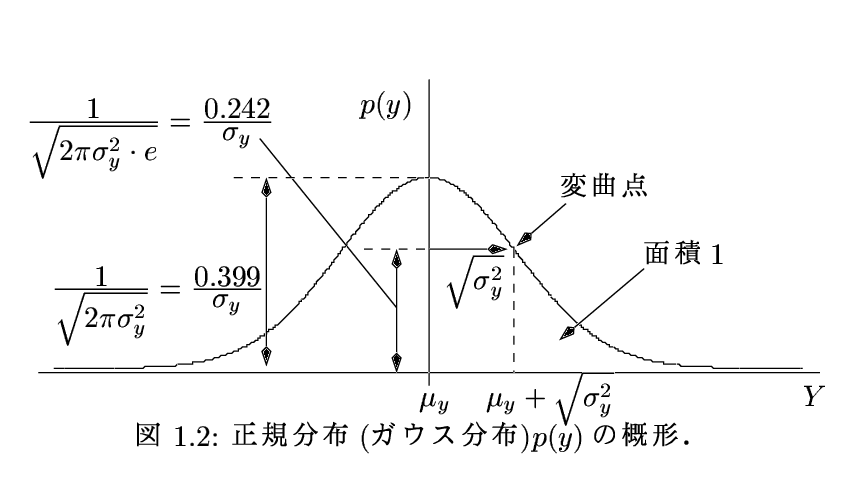
| 3 | 図1.2 | 図1.2参照 | |
| 17 | 下から3行目 | 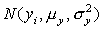 |
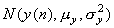 |
| 31 | 3行目 | 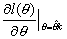 と と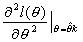 を を |
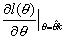 と と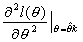 は は |
| 33 | 下から5行目 | 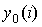 |
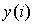 |
| 42 | 4行目 | 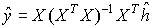 |
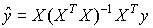 |
| 55 | 図2.7 | 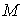 次元実空間 次元実空間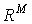 |
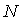 次元実空間 次元実空間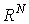 |
| 56 | 図2.8の説明文 | 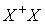 |
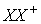 |
| 58 | 5行目 | 正規直交系† | 正規直交系†1 |
| 下から1行目 | といい, | といい†2, | |
| 脚注1行目 | † | †1 | |
| 脚注2〜3行目 | を表している。 | を表す。 | |
| 脚注 | 脚注2として下記を追加 †2 orthogonalは直交の意味で,通常「直交行列」と訳されるが,性質は正 規直交(orthonormal)であるので,本書では「正規直交行列」としている。 |
||
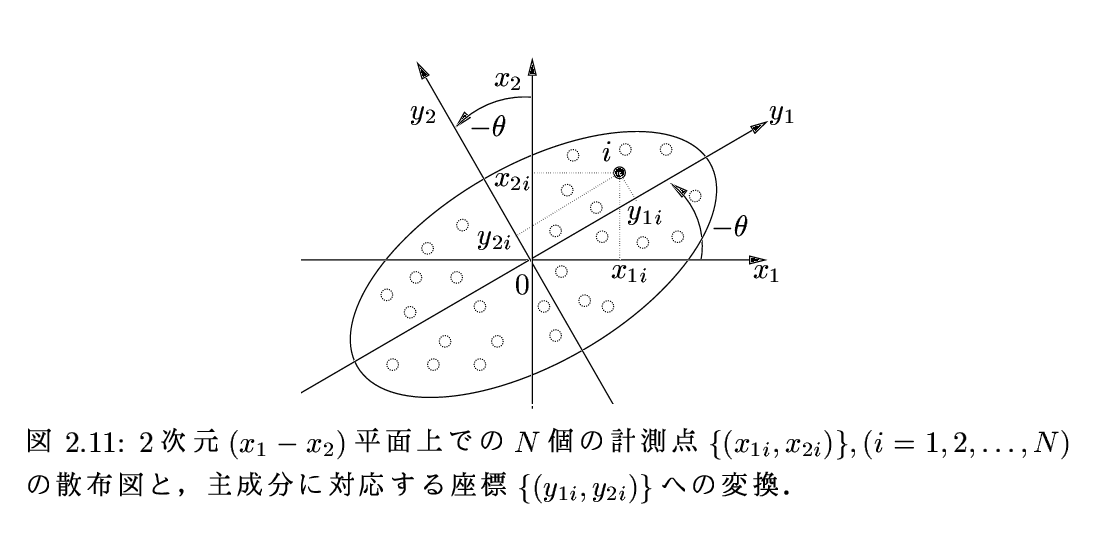
| 68 | 図2.11 | 図2.11参照 | |
| 71 | 9行目 | 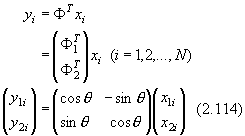 |
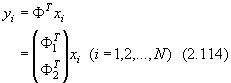 |
| 74 | 5行目 | 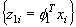 |
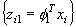 |
| 75 | 下から4行目 | 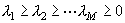 |
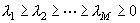 |
| 脚注1の3行目 | constaint least squares method | constaint least-squares method | |
| 76 | 3行目 | この式から | この式と とから とから |
| 77 | 3行目 | 掛けると | 掛けて式(2.136)を用いると, |
| 79 | 8行目 | 行列Σ | 共分散行列Σ |
| 80 | 下から3行目 | 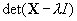 |
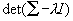 |
| 下から1行目 | 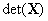 |
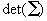 |
|
| 81 | 1〜3行目 | X | Σ |
| 下から1行目 | 正則行列 | 正則行列W | |
| 83 | 9行目 | 式(2.156)から, | 式(2.156)より, |
| 84 | 5行目 | 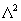 や や |
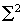 や や |
| 85 | 下から5行目 | 下記を追加 行列Yの列は, 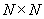 行列 行列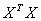 の固有ベクトルとなる。 の固有ベクトルとなる。 |
|
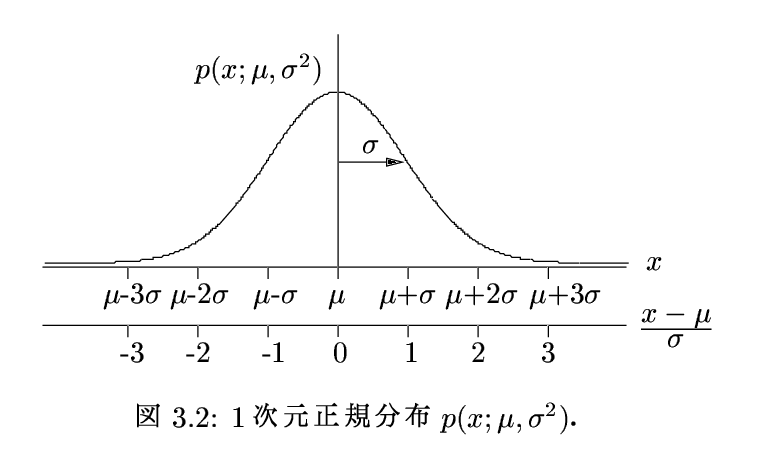
| 94 | 図3.2 | 図3.2参照 | |
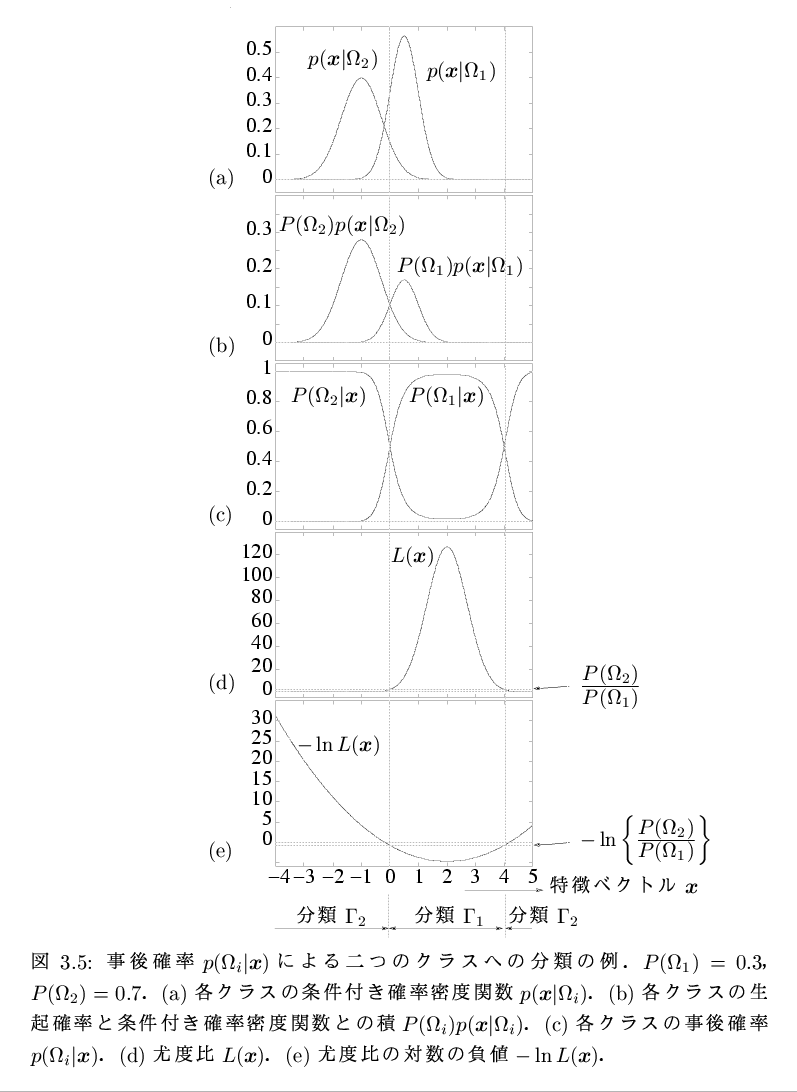
| 99 | 図3.5 | 図3.5参照 | |
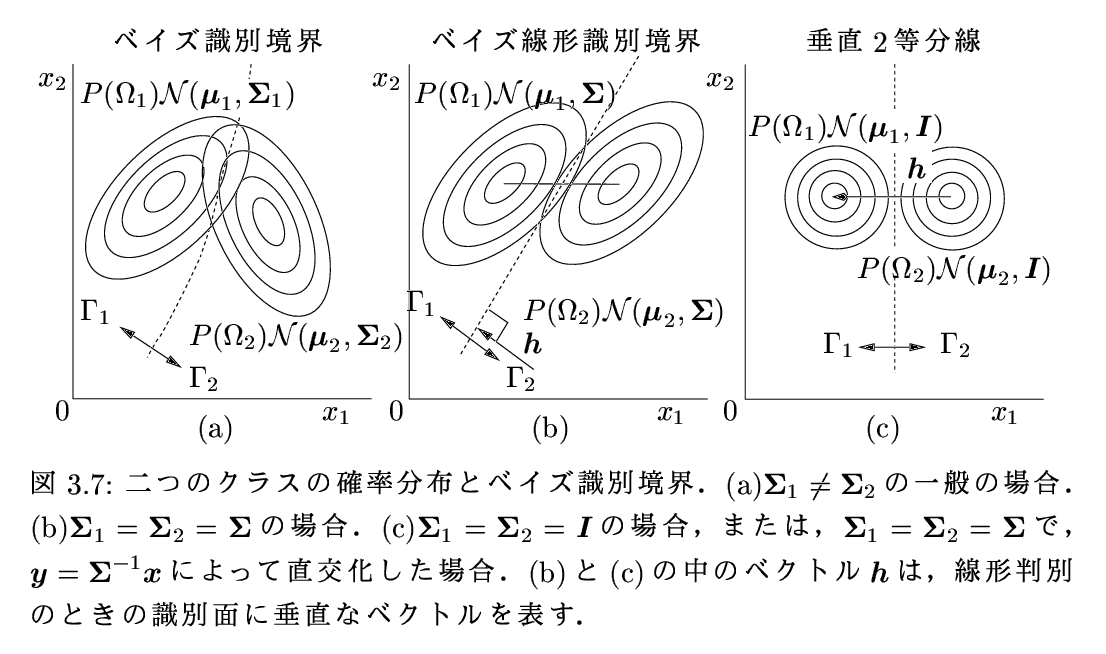
| 101 | 図3.7 | 図3.7参照 | |
| 117 | 2行目 | 極を,z=0に零点をもつ†。 | 極をもつ†。 |
| 142 | 脚注1の7行目 | 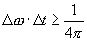 または または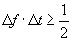 |
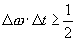 または または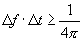 |
| 151 | 1行目 | 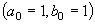 |
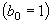 |
| 155 | 下から5行目 | 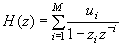 |
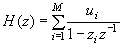 |
| 158 | 6行目 | 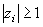 |
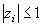 |
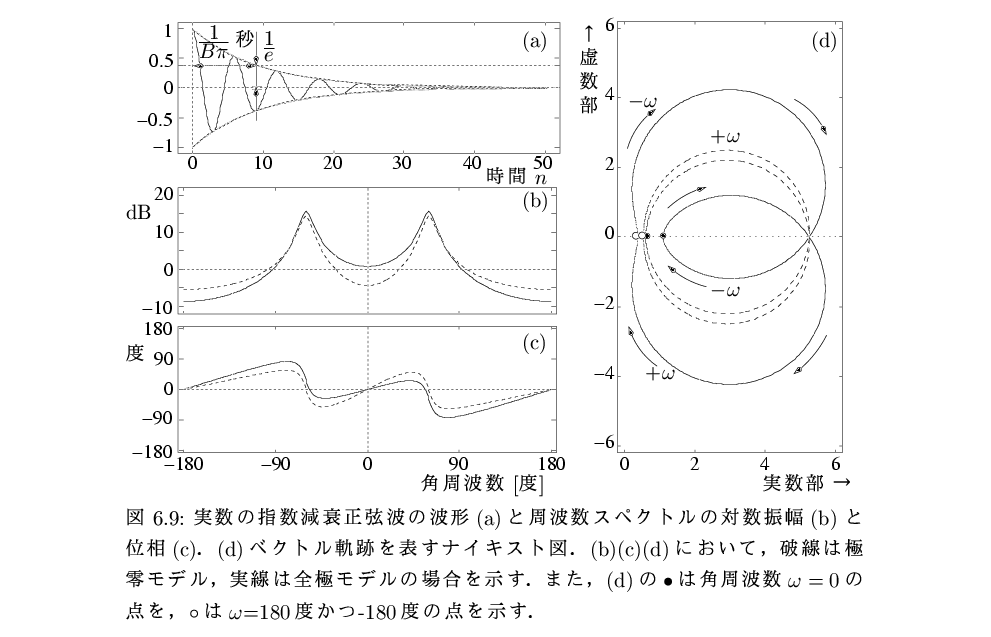
| 図6.9 | 図6.9参照 | ||
| 162 | 1行目 | スティッフネス | スティフネス |
| 脚注1 | スティッフネス | スティフネス | |
| 164 | 表6.1下から3行目 | インピーダンスY= | アドミッタンスY= |
| 6行目 | 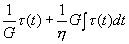 |
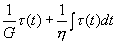 |
|
| 170 | 2行目 | 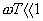 と と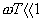 の の |
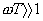 と と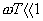 の の |
| 4行目 | 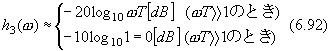 |
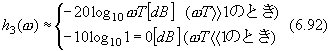 |
|
| 171 | 下から9行目 | 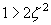 と と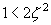 の の |
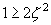 と と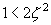 の の |
| 下から8行目 | 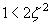 のとき のとき |
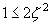 のとき のとき |
|
| 259 | 下から1行目 | 定値 | 次頁1行目へ移動 |
| 263 | 3行目 | 振幅二乗コヒーレンス関数をによって | 振幅二乗コヒーレンス関数によって |
| 269 | 下から2行目 | そのた, | そのため, |
| 275 | 1行目 | magnitude-sqared | magnitude-squared |
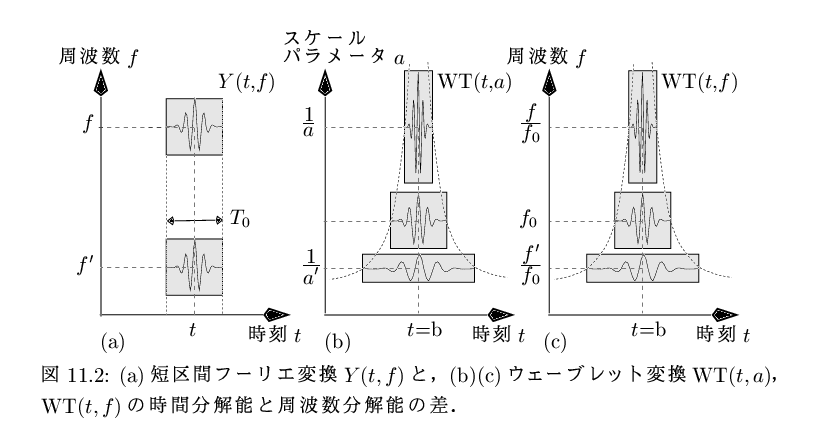
| 298 | 図11.2 | 図11.2参照 | |
| 300 | 図11.4 | 図11.4参照 | |
| 306 | 図11.6の説明文 | 式(11.18)離散的短区間 | 式(11.18)の離散的短区間 |
| 307 | 4行目 | これは式(6.21)の | これは式(6.16)の |
| 325 | 左側下から7行目 | 121,124,256 | 122,124,256 |